Category: Complexity
Equalized Hyperspin Machine
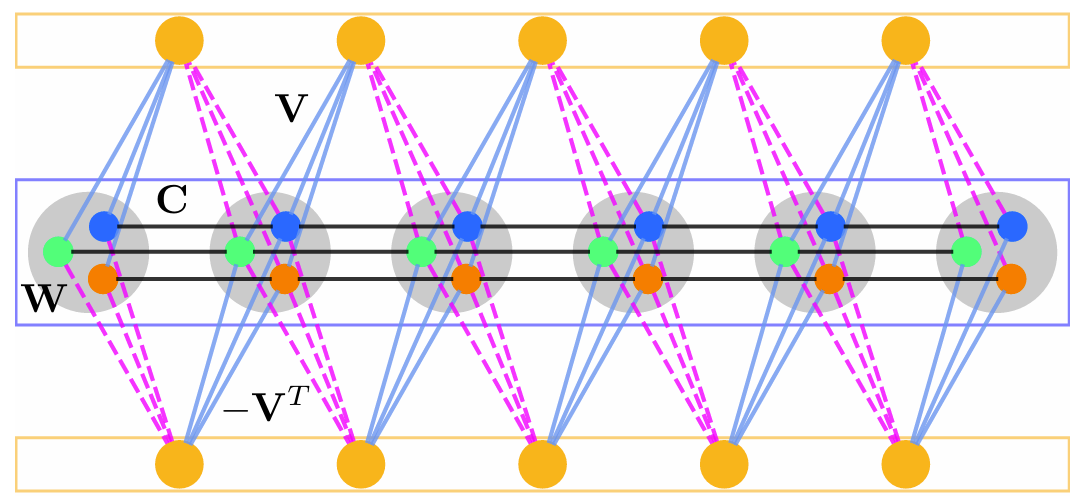
The reliable simulation of spin models is of critical importance to tackle complex optimization problems that are intractable on conventional computing machines. The recently introduced hyperspin machine, which is a network of linearly and nonlinearly coupled parametric oscillators, provides a versatile simulator of general classical vector spin models in arbitrary dimension, finding the minimum of the simulated spin Hamiltonian and implementing novel annealing algorithms. In the hyperspin machine, oscillators evolve in time minimizing a cost function that must resemble the desired spin Hamiltonian in order for the system to reliably simulate the target spin model. This condition is met if the hyperspin amplitudes are equal in the steady state. Currently, no mechanism to enforce equal amplitudes exists. Here, we bridge this gap and introduce a method to simulate the hyperspin machine with equalized amplitudes in the steady state. We employ an additional network of oscillators (named equalizers) that connect to the hyperspin machine via an antisymmetric nonlinear coupling and equalize the hyperspin amplitudes. We demonstrate the performance of such an equalized hyperspin machine by large-scale numerical simulations up to 10000 hyperspins. Compared to the hyperspin machine without equalization, we find that the equalized hyperspin machine (i) Reaches orders of magnitude lower spin energy, and (ii) Its performance is significantly less sensitive to the system parameters. The equalized hyperspin machine offers a competitive spin Hamiltonian minimizer and opens the possibility to combine amplitude equalization with complex annealing protocols to further boost the performance of spin machines.
The First Experimental Observation of Ultrametricity
https://www.researchsquare.com/article/rs-5433512/v1
Ultrametricity is a fundamental mathematical concept that describes a particular metric space in which every triplet of points in the space forms an isosceles triangle. The ultrametric space differs from the usual Archimedean metric, where three points are allowed from any triangle.
Ultrametricity is the topology of hierarchical architectures. Examples can be found in taxonomy, where phylogenetic trees are ultrametric, mathematics with p-adic numbers, geography for measuring landscape complexity, and physics, where complex systems have intrinsically an ultrametric structure.
The Noble Prize Giorgio Parisi demonstrated this within the theory of spin glasses, where the overlap between spins exhibits ultrametricity, with the mathematical solution given by the full replica symmetry breaking.
An experimental demonstration of this is still lacking due to the difficulty of finding measurable physical observables.
In 2015, we introduced random lasers as photonic counterparts of spin glasses, and we demonstrated the replica symmetry breaking by directly measuring the overlap between spins, known as the order parameter in the description of glass phase transitions.
In the work, we clearly show the hierarchical organization of the overlap matrix reproducing the Parisi Ansatz, and we experimentally prove the ultrametric nature of the replica states.
For the first time, we measure the distance between any three replicas forming a triangle, and we report the growth of the distribution of isosceles tringles when the system enters the glassy regime. This is an unambiguous way to demonstrate ultrametricity and has been previously done only in numerical simulations.
In addition, from the hierarchical structure of the spin states, illustrated as dendrograms, and the distances between replicas, we attain the first topological energy landscape of a complex system from experiments.
The great potentiality of our research is the ability to access measurable spins from emission spectra and to quantify the overlap parameter. Random lasers are photonic spin glasses, as they manifest a clear phase transition from a paramagnetic ordered state to a glassy disordered one by increasing the system’s energy. Thanks to this powerful asset, we demonstrate the ultrametricity of the replica space. We report the experimental energy landscape with a topology that changes from a flat large basin to the coexistence of many metastable minima and the braking of ergodicity in the glassy state.
Emergent Equilibrium in All-Optical Single Quantum-Trajectory Ising Machines
We investigate the dynamics of multi-mode optical systems driven by two-photon processes and subject to non-local losses, incorporating quantum noise at the Gaussian level. Our findings show that the statistics from a single Gaussian quantum trajectory exhibit emergent thermal equilibrium governed by an Ising Hamiltonian encoded in the dissipative coupling between modes. The driving strength sets the system’s effective temperature relative to the oscillation threshold. Given the ultra-short time scales typical of all-optical devices, our study demonstrates that such multi-mode optical systems can operate as ultra-fast Boltzmann samplers, paving the way toward the realization of efficient hardware for combinatorial optimization, with promising applications in machine learning and beyond.
Fully Programmable Spatial Photonic Ising Machine by Focal Plane Division
https://arxiv.org/abs/2410.10689
Ising machines are an emerging class of hardware that promises ultrafast and energy-efficient solutions to NP-hard combinatorial optimization problems. Spatial photonic Ising machines (SPIMs) exploit optical computing in free space to accelerate the computation, showcasing parallelism, scalability, and low power consumption. However, current SPIMs can implement only a restricted class of problems. This partial programmability is a critical limitation that hampers their benchmark. Achieving full programmability of the device while preserving its scalability is an open challenge. Here, we report a fully programmable SPIM achieved through a novel operation method based on the division of the focal plane. In our scheme, a general Ising problem is decomposed into a set of Mattis Hamiltonians, whose energies are simultaneously computed optically by measuring the intensity on different regions of the camera sensor. Exploiting this concept, we experimentally demonstrate the computation with high success probability of ground-state solutions of up to 32-spin Ising models on unweighted maximum cut graphs with and without ferromagnetic bias. Simulations of the hardware prove a favorable scaling of the accuracy with the number of spins. Our fully programmable SPIM enables the implementation of many quadratic unconstrained binary optimization problems, further establishing SPIMs as a leading paradigm in non von Neumann hardware.