https://doi.org/10.1103/ggbs-y21w
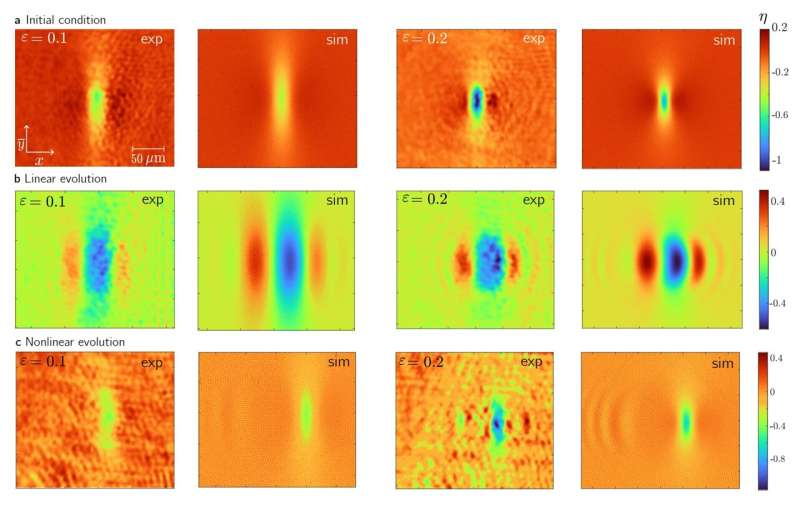
Solitons are the cornerstone of nonlinear physics. The integrability of nonlinear equations is the basis of this universal concept. However, most multidimensional systems lack integrability, a fundamental limitation that challenges the existence of solitons in high dimensions. A remarkable exception would be the lump soliton, a two-dimensional solution of the Kadomtsev-Petviashvili (KP) equation with the unique property of propagating unperturbed in three-dimensional space. Due to the difficulty of implementing the KP dynamics in any physical system, lump solitons have never been observed. Here, we report the first experimental observation of the lump soliton. The lump is realized in nonlinear optics, in a photorefractive crystal under the action of paraxial diffraction and defocusing nonlinearity, ruled by the (2+1)D nonlinear Schrödinger (NLS) equation. We tailor the input field shape and the nonlinearity to realize the hydrodynamic KP integrable regime of the NLS equation. The lump emerges as a self-localized wave that propagates unaltered with a transverse velocity. We confirm its integrable nature by reporting, for the first time, the elastic collision of lumps in two dimensions. As the first experimental evidence of integrable solitons in high dimensions, our observation paves the way for a new era in the study of nonlinear systems.
Featured in Physics, Editors’suggestion
https://physics.aps.org/articles/v19/s22
https://phys.org/news/2026-01-physicists-resilient-3d-solitons-lab.html