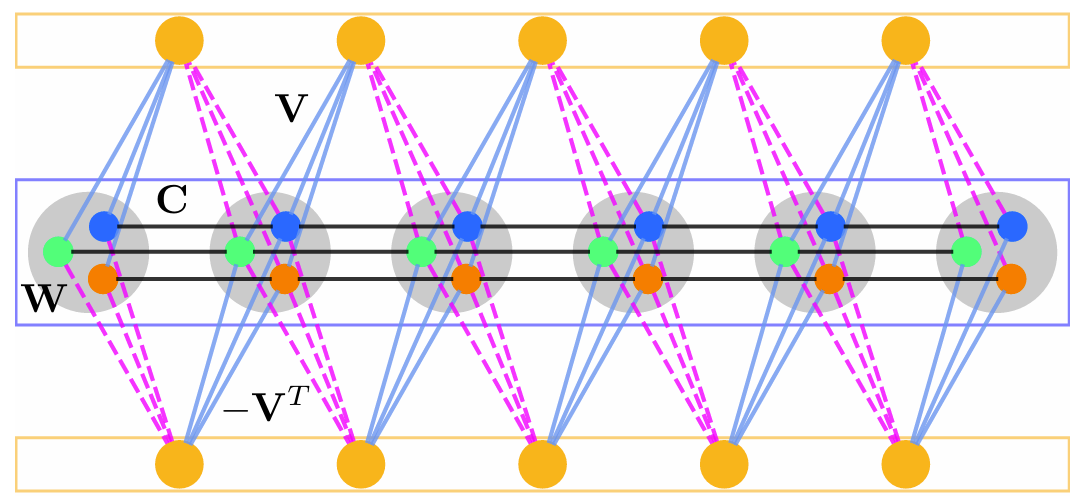
The reliable simulation of spin models is of critical importance to tackle complex optimization problems that are intractable on conventional computing machines. The recently introduced hyperspin machine, which is a network of linearly and nonlinearly coupled parametric oscillators, provides a versatile simulator of general classical vector spin models in arbitrary dimension, finding the minimum of the simulated spin Hamiltonian and implementing novel annealing algorithms. In the hyperspin machine, oscillators evolve in time minimizing a cost function that must resemble the desired spin Hamiltonian in order for the system to reliably simulate the target spin model. This condition is met if the hyperspin amplitudes are equal in the steady state. Currently, no mechanism to enforce equal amplitudes exists. Here, we bridge this gap and introduce a method to simulate the hyperspin machine with equalized amplitudes in the steady state. We employ an additional network of oscillators (named equalizers) that connect to the hyperspin machine via an antisymmetric nonlinear coupling and equalize the hyperspin amplitudes. We demonstrate the performance of such an equalized hyperspin machine by large-scale numerical simulations up to 10000 hyperspins. Compared to the hyperspin machine without equalization, we find that the equalized hyperspin machine (i) Reaches orders of magnitude lower spin energy, and (ii) Its performance is significantly less sensitive to the system parameters. The equalized hyperspin machine offers a competitive spin Hamiltonian minimizer and opens the possibility to combine amplitude equalization with complex annealing protocols to further boost the performance of spin machines.
Category: Coding
About coding in any language
Deep Learning Enabled Transmission of Full-Stokes Polarization Images Through Complex Media
Polarization images offer crucial functionalities across multiple scientific domains, providing access to physical information beyond conventional measures such as intensity, phase, and spectrum of light. However, the challenge of transmitting polarization images through complex media has restricted their application in optical communication and imaging. Here, a novel approach utilizing deep learning for the transmission of full-Stokes polarization images through scattering media is presented. It is demonstrated that any input polarization image can be reconstructed in a single shot by employing only an intensity sensor. By supervised training of a deep neural network, high-accuracy full-Stokes reconstruction is achieved from the speckle pattern detected by an intensity camera. Leveraging the deep learning based polarization decoder, a polarization-colored encoding scheme is devised to enable increased-capacity data transmission through disordered channels. Fast, wavelength-independent, on-chip, polarization imaging in complex media enables the utilization of polarization-structured light in multimode fibres and opaque materials, unlocking new possibilities in optical communication, cryptography, and quantum technology.
Non-Gaussianity in the quantum parametric oscillator
https://journals.aps.org/pra/abstract/10.1103/PhysRevA.109.063519
Systems of coupled optical parametric oscillators (OPOs) forming an Ising machine are emerging as large-scale simulators of the Ising model. The advances in computer science and nonlinear optics have triggered not only the physical realization of hybrid (electrooptical) or all-optical Ising machines, but also the demonstration of quantum-inspired algorithms boosting their performances. To date, the use of the quantum nature of parametrically generated light as a further resource for computation represents a major open issue. A key quantum feature is the non-Gaussian character of the system state across the oscillation threshold. In this paper, we perform an ab initio analysis of the emergence of non-Gaussianity in the single quantum OPO with an applied external field. We model the OPO by a Lindblad master equation, which is numerically solved by a first-principles method based on exact diagonalization. Non-Gaussianity is quantified by means of three different metrics: the Hilbert-Schmidt distance, quantum relative entropy, and photon distribution. Our findings reveal a nontrivial interplay between parametric drive and applied field: (i) the increasing pump monotonically enhances non-Gaussianity and (ii) the increasing field first sharpens non-Gaussianity, and then restores the Gaussian character of the state when above a threshold value. We also report a first-principles computation in the Fock space of the distance from the mixture of coherent states, a strongly nonclassical behavior that can play a significant role in the quantum parallel search for optimization.
See also arXiv
Inverse design of high-dimensional quantum optical circuits in Nature Physics !
Programmable optical circuits are an important tool in developing quantum technologies such as transceivers for quantum communication and integrated photonic chips for quantum information processing. Maintaining precise control over every individual component becomes challenging at large scales, leading to a reduction in the quality of operations performed. In parallel, minor imperfections in circuit fabrication are amplified in this regime, dramatically inhibiting their performance. Here we use inverse design techniques to embed optical circuits in the higher-dimensional space of a large, ambient mode mixer such as a commercial multimode fibre. This approach allows us to forgo control over each individual circuit element, and retain a high degree of programmability. We use our circuits as quantum gates to manipulate high-dimensional spatial-mode entanglement in up to seven dimensions. Their programmability allows us to turn a multimode fibre into a generalized multioutcome measurement device, allowing us to both transport and certify entanglement within the transmission channel. With the support of numerical simulations, we show that our method is a scalable approach to obtaining high circuit fidelity with a low circuit depth by harnessing the resource of a high-dimensional mode mixer.
https://www.nature.com/articles/s41567-023-02319-6
Highlight in Phys.org
See also Quantum Gates by TensorFlow and Reservoir Computing
Dawn and fall of non-Gaussianity in the quantum parametric oscillator
Systems of coupled optical parametric oscillators (OPOs) forming an Ising machine are emerging as large-scale simulators of the Ising model. The advances in computer science and nonlinear optics have triggered not only the physical realization of hybrid (electro-optical) or all-optical Ising machines, but also the demonstration of quantum-inspired algorithms boosting their performances. To date, the use of the quantum nature of parametrically generated light as a further resource for computation represents a major open issue. A key quantum feature is the non-Gaussian character of the system state across the oscillation threshold. In this paper, we perform an extensive analysis of the emergence of non-Gaussianity in the single quantum OPO with an applied external field. We model the OPO by a Lindblad master equation, which is numerically solved by an ab initio method based on exact diagonalization. Non-Gaussianity is quantified by means of three different metrics: Hilbert-Schmidt distance, quantum relative entropy, and photon distribution. Our findings reveal a nontrivial interplay between parametric drive and applied field: (i) Increasing pump monotonously enhances non-Gaussianity, and (ii) Increasing field first sharpens non-Gaussianity, and then restores the Gaussian character of the state when above a threshold value.