Category: Nonlinear Photonics

Particle trajectories in light pulse spacetime

https://arxiv.org/abs/2507.20203

In our previous work (Phys. Rev. Research 7, 033079), we derived the metric tensor for cylindrically shaped pulses with uniform energy density. Building upon that framework, we derive the complete set of geodesics with zero angular velocity. We show that perturbations in particle trajectories may be observed in gamma ray bursts. Also, deviations in the motion of moving particles are significantly larger than those previously found for particles that are initially at rest.

Ising Machine by Dimensional Collapse of Nonlinear Polarization Oscillators

https://journals.aps.org/prl/abstract/10.1103/qs29-2xqc

Phys. Rev. Lett. 135, 063801 – Published 4 August, 2025

Ising machines show promise as ultrafast hardware for optimizations encoded in Ising Hamiltonians but fall short in terms of success rate and performance scaling. Here, we propose a novel Ising machine that exploits the three-dimensional nature of nonlinear polarization oscillators to counteract these limitations. Based on the evolution of the optical polarization in third-order nonlinear media, the high-dimensional machine reaches the Ising ground state by the mechanism of “dimensional collapse”: the dynamics on the Poincaré sphere undergoes a self-induced collapse into polarization fixed points mapping an Ising spin. Collapse from a spherical to a binary spin occurs when the polarization oscillator experiences iterative loss and anisotropic feedback. The photonic setup consists of polarization modulated pulses in a 𝜒(3) crystal subject to measurement and feedback. We numerically demonstrate the polarization machine achieves enhanced success probability on benchmark graphs and an exponential improvement in performance scaling with respect to coherent Ising machines due to its high-dimensional operation. The proposed Ising machine paves the way for a new class of Ising solvers with enhanced computing capabilities.

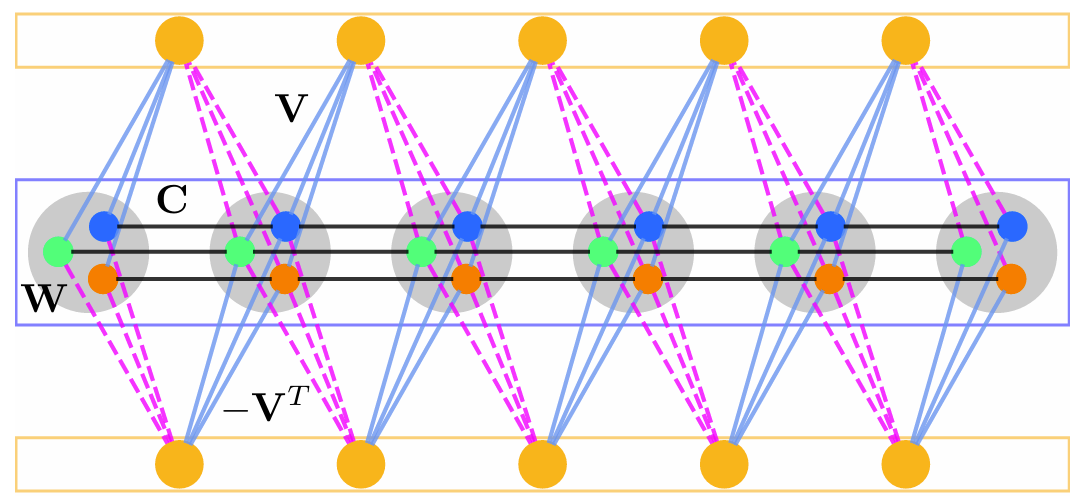
Equalized Hyperspin Machine

The reliable simulation of spin models is of critical importance to tackle complex optimization problems that are intractable on conventional computing machines. The recently introduced hyperspin machine, which is a network of linearly and nonlinearly coupled parametric oscillators, provides a versatile simulator of general classical vector spin models in arbitrary dimension, finding the minimum of the simulated spin Hamiltonian and implementing novel annealing algorithms. In the hyperspin machine, oscillators evolve in time minimizing a cost function that must resemble the desired spin Hamiltonian in order for the system to reliably simulate the target spin model. This condition is met if the hyperspin amplitudes are equal in the steady state. Currently, no mechanism to enforce equal amplitudes exists. Here, we bridge this gap and introduce a method to simulate the hyperspin machine with equalized amplitudes in the steady state. We employ an additional network of oscillators (named equalizers) that connect to the hyperspin machine via an antisymmetric nonlinear coupling and equalize the hyperspin amplitudes. We demonstrate the performance of such an equalized hyperspin machine by large-scale numerical simulations up to 10000 hyperspins. Compared to the hyperspin machine without equalization, we find that the equalized hyperspin machine (i) Reaches orders of magnitude lower spin energy, and (ii) Its performance is significantly less sensitive to the system parameters. The equalized hyperspin machine offers a competitive spin Hamiltonian minimizer and opens the possibility to combine amplitude equalization with complex annealing protocols to further boost the performance of spin machines.

[2507.12940] Equalized Hyperspin Machine

Phys. Rev. A 112, 053505 (2025)

Cumulative effects of laser-generated gravitational shock waves

https://arxiv.org/abs/2503.05001

https://journals.aps.org/prresearch/abstract/10.1103/ylvn-3ybm

The emission of light pulses is expected to generate gravitational waves, opening the possibility of controlling gravity in an Earthed laboratory. However, measuring the optically-driven spacetime deformations is challenging due to the inherently weak interaction. We explore the possibility to achieve a detectable gravitational effect from light emission by examining the cumulative effect of a sequence of laser-generated gravitational shock waves on a test particle. We derive an exact solution to the Einstein equations for cylindrically-shaped optical beams with constant energy density, imposing continuity condition for the metric and its first-order derivatives. Our analysis reveals that laser-induced gravitational fields cause a spatial shift in the test particle, which is measurable within current interferometric technology.

Emergent Equilibrium in All-Optical Single Quantum-Trajectory Ising Machines

We investigate the dynamics of multi-mode optical systems driven by two-photon processes and subject to non-local losses, incorporating quantum noise at the Gaussian level. Our findings show that the statistics from a single Gaussian quantum trajectory exhibit emergent thermal equilibrium governed by an Ising Hamiltonian encoded in the dissipative coupling between modes. The driving strength sets the system’s effective temperature relative to the oscillation threshold. Given the ultra-short time scales typical of all-optical devices, our study demonstrates that such multi-mode optical systems can operate as ultra-fast Boltzmann samplers, paving the way toward the realization of efficient hardware for combinatorial optimization, with promising applications in machine learning and beyond.

https://arxiv.org/abs/2412.12768

https://mathstodon.xyz/@nonlinearxwaves/113672283856089363