Category: ERC-AdG HYPERSPIM

Observation of Lump Solitons — after 50 years

https://doi.org/10.1103/ggbs-y21w

Solitons are the cornerstone of nonlinear physics. The integrability of nonlinear equations is the basis of this universal concept. However, most multidimensional systems lack integrability, a fundamental limitation that challenges the existence of solitons in high dimensions. A remarkable exception would be the lump soliton, a two-dimensional solution of the Kadomtsev-Petviashvili (KP) equation with the unique property of propagating unperturbed in three-dimensional space. Due to the difficulty of implementing the KP dynamics in any physical system, lump solitons have never been observed. Here, we report the first experimental observation of the lump soliton. The lump is realized in nonlinear optics, in a photorefractive crystal under the action of paraxial diffraction and defocusing nonlinearity, ruled by the (2+1)⁢D nonlinear Schrödinger (NLS) equation. We tailor the input field shape and the nonlinearity to realize the hydrodynamic KP integrable regime of the NLS equation. The lump emerges as a self-localized wave that propagates unaltered with a transverse velocity. We confirm its integrable nature by reporting, for the first time, the elastic collision of lumps in two dimensions. As the first experimental evidence of integrable solitons in high dimensions, our observation paves the way for a new era in the study of nonlinear systems.

Featured in Physics, Editors’suggestion

https://physics.aps.org/articles/v19/s22

https://phys.org/news/2026-01-physicists-resilient-3d-solitons-lab.html

Ising Machine by Dimensional Collapse of Nonlinear Polarization Oscillators

https://journals.aps.org/prl/abstract/10.1103/qs29-2xqc

Phys. Rev. Lett. 135, 063801 – Published 4 August, 2025

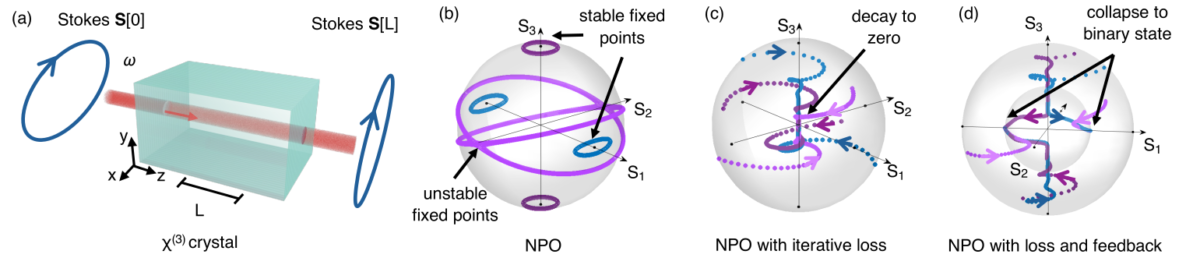
Ising machines show promise as ultrafast hardware for optimizations encoded in Ising Hamiltonians but fall short in terms of success rate and performance scaling. Here, we propose a novel Ising machine that exploits the three-dimensional nature of nonlinear polarization oscillators to counteract these limitations. Based on the evolution of the optical polarization in third-order nonlinear media, the high-dimensional machine reaches the Ising ground state by the mechanism of “dimensional collapse”: the dynamics on the Poincaré sphere undergoes a self-induced collapse into polarization fixed points mapping an Ising spin. Collapse from a spherical to a binary spin occurs when the polarization oscillator experiences iterative loss and anisotropic feedback. The photonic setup consists of polarization modulated pulses in a 𝜒(3) crystal subject to measurement and feedback. We numerically demonstrate the polarization machine achieves enhanced success probability on benchmark graphs and an exponential improvement in performance scaling with respect to coherent Ising machines due to its high-dimensional operation. The proposed Ising machine paves the way for a new class of Ising solvers with enhanced computing capabilities.

Equalized Hyperspin Machine

The reliable simulation of spin models is of critical importance to tackle complex optimization problems that are intractable on conventional computing machines. The recently introduced hyperspin machine, which is a network of linearly and nonlinearly coupled parametric oscillators, provides a versatile simulator of general classical vector spin models in arbitrary dimension, finding the minimum of the simulated spin Hamiltonian and implementing novel annealing algorithms. In the hyperspin machine, oscillators evolve in time minimizing a cost function that must resemble the desired spin Hamiltonian in order for the system to reliably simulate the target spin model. This condition is met if the hyperspin amplitudes are equal in the steady state. Currently, no mechanism to enforce equal amplitudes exists. Here, we bridge this gap and introduce a method to simulate the hyperspin machine with equalized amplitudes in the steady state. We employ an additional network of oscillators (named equalizers) that connect to the hyperspin machine via an antisymmetric nonlinear coupling and equalize the hyperspin amplitudes. We demonstrate the performance of such an equalized hyperspin machine by large-scale numerical simulations up to 10000 hyperspins. Compared to the hyperspin machine without equalization, we find that the equalized hyperspin machine (i) Reaches orders of magnitude lower spin energy, and (ii) Its performance is significantly less sensitive to the system parameters. The equalized hyperspin machine offers a competitive spin Hamiltonian minimizer and opens the possibility to combine amplitude equalization with complex annealing protocols to further boost the performance of spin machines.

[2507.12940] Equalized Hyperspin Machine

Phys. Rev. A 112, 053505 (2025)