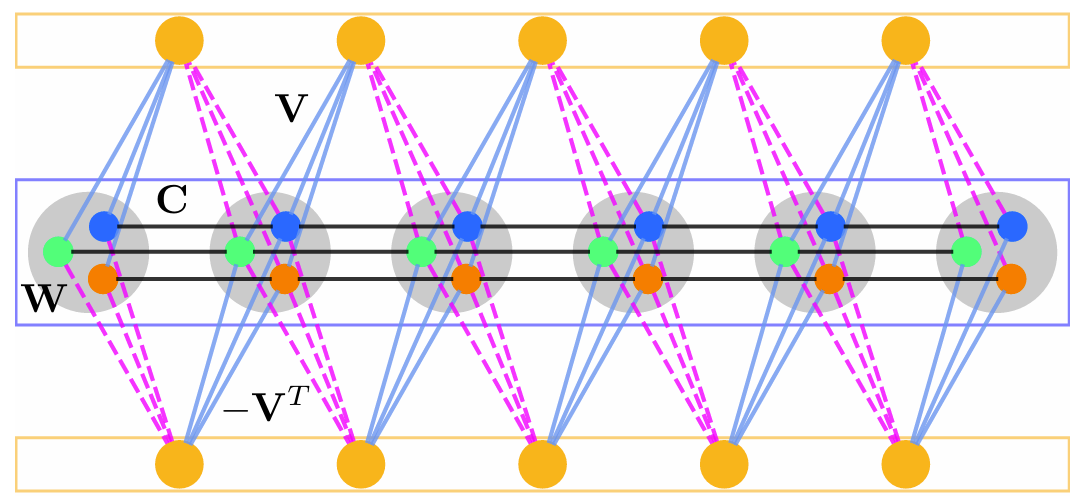
The reliable simulation of spin models is of critical importance to tackle complex optimization problems that are intractable on conventional computing machines. The recently introduced hyperspin machine, which is a network of linearly and nonlinearly coupled parametric oscillators, provides a versatile simulator of general classical vector spin models in arbitrary dimension, finding the minimum of the simulated spin Hamiltonian and implementing novel annealing algorithms. In the hyperspin machine, oscillators evolve in time minimizing a cost function that must resemble the desired spin Hamiltonian in order for the system to reliably simulate the target spin model. This condition is met if the hyperspin amplitudes are equal in the steady state. Currently, no mechanism to enforce equal amplitudes exists. Here, we bridge this gap and introduce a method to simulate the hyperspin machine with equalized amplitudes in the steady state. We employ an additional network of oscillators (named equalizers) that connect to the hyperspin machine via an antisymmetric nonlinear coupling and equalize the hyperspin amplitudes. We demonstrate the performance of such an equalized hyperspin machine by large-scale numerical simulations up to 10000 hyperspins. Compared to the hyperspin machine without equalization, we find that the equalized hyperspin machine (i) Reaches orders of magnitude lower spin energy, and (ii) Its performance is significantly less sensitive to the system parameters. The equalized hyperspin machine offers a competitive spin Hamiltonian minimizer and opens the possibility to combine amplitude equalization with complex annealing protocols to further boost the performance of spin machines.
Cumulative effects of laser-generated gravitational shock waves
https://arxiv.org/abs/2503.05001
https://journals.aps.org/prresearch/abstract/10.1103/ylvn-3ybm
The emission of light pulses is expected to generate gravitational waves, opening the possibility of controlling gravity in an Earthed laboratory. However, measuring the optically-driven spacetime deformations is challenging due to the inherently weak interaction. We explore the possibility to achieve a detectable gravitational effect from light emission by examining the cumulative effect of a sequence of laser-generated gravitational shock waves on a test particle. We derive an exact solution to the Einstein equations for cylindrically-shaped optical beams with constant energy density, imposing continuity condition for the metric and its first-order derivatives. Our analysis reveals that laser-induced gravitational fields cause a spatial shift in the test particle, which is measurable within current interferometric technology.

The solution to energy demanding artificial intelligence : optical neural networks with solar cells
https://www.researching.cn/articles/OJ930a39ae0105db58
https://opg.optica.org/prj/abstract.cfm?doi=10.1364/PRJ.542564
Optical neural networks (ONNs) are a class of emerging computing platforms that leverage the properties of light to perform ultra-fast computations with ultra-low energy consumption. ONNs often use CCD cameras as the output layer. In this work, we propose the use of perovskite solar cells as a promising alternative to imaging cameras in ONN designs. Solar cells are ubiquitous, versatile, highly customizable, and can be fabricated quickly in laboratories. Their large acquisition area and outstanding efficiency enable them to generate output signals with a large dynamic range without the need for amplification. Here we have experimentally demonstrated the feasibility of using perovskite solar cells for capturing ONN output states, as well as the capability of single-layer random ONNs to achieve excellent performance even with a very limited number of pixels. Our results show that the solar-cell-based ONN setup consistently outperforms the same setup with CCD cameras of the same resolution. These findings highlight the potential of solar-cell-based ONNs as an ideal choice for automated and battery-free edge-computing applications.
The First Experimental Observation of Ultrametricity
https://www.researchsquare.com/article/rs-5433512/v1
Ultrametricity is a fundamental mathematical concept that describes a particular metric space in which every triplet of points in the space forms an isosceles triangle. The ultrametric space differs from the usual Archimedean metric, where three points are allowed from any triangle.
Ultrametricity is the topology of hierarchical architectures. Examples can be found in taxonomy, where phylogenetic trees are ultrametric, mathematics with p-adic numbers, geography for measuring landscape complexity, and physics, where complex systems have intrinsically an ultrametric structure.
The Noble Prize Giorgio Parisi demonstrated this within the theory of spin glasses, where the overlap between spins exhibits ultrametricity, with the mathematical solution given by the full replica symmetry breaking.
An experimental demonstration of this is still lacking due to the difficulty of finding measurable physical observables.
In 2015, we introduced random lasers as photonic counterparts of spin glasses, and we demonstrated the replica symmetry breaking by directly measuring the overlap between spins, known as the order parameter in the description of glass phase transitions.
In the work, we clearly show the hierarchical organization of the overlap matrix reproducing the Parisi Ansatz, and we experimentally prove the ultrametric nature of the replica states.
For the first time, we measure the distance between any three replicas forming a triangle, and we report the growth of the distribution of isosceles tringles when the system enters the glassy regime. This is an unambiguous way to demonstrate ultrametricity and has been previously done only in numerical simulations.
In addition, from the hierarchical structure of the spin states, illustrated as dendrograms, and the distances between replicas, we attain the first topological energy landscape of a complex system from experiments.
The great potentiality of our research is the ability to access measurable spins from emission spectra and to quantify the overlap parameter. Random lasers are photonic spin glasses, as they manifest a clear phase transition from a paramagnetic ordered state to a glassy disordered one by increasing the system’s energy. Thanks to this powerful asset, we demonstrate the ultrametricity of the replica space. We report the experimental energy landscape with a topology that changes from a flat large basin to the coexistence of many metastable minima and the braking of ergodicity in the glassy state.