Category: Projects
An inequality for relativistic local quantum measurements
We investigate the trade-off between vacuum insensitivity and sensitivity to excitations in finite-size detectors, taking measurement locality as a fundamental constraint. We derive an upper bound on the detectability of vacuum excitation, given a small but nonzero probability of false positives in the vacuum state. The result is independent of the specific details of the measurement or the underlying physical mechanisms of the detector and relies only on the assumption of locality. Experimental confirmation or violation of the inequality would provide a test of the axioms of algebraic quantum field theory, offer new insights into the measurement problem in relativistic quantum physics, and establish a fundamental technological limit in local particle detection.
Reeh-Schlieder approximation for coherent states
We present an explicit, fully local Reeh-Schlieder approximation scheme for coherent states of a free scalar field. For any bounded region U, we construct a one-parameter family of bounded operators A^ζ localized in the causal complement of U. The action of A^ζ on the vacuum approximates the target coherent state in the limit ζ→0.
Particle trajectories in light pulse spacetime
https://arxiv.org/abs/2507.20203
In our previous work (Phys. Rev. Research 7, 033079), we derived the metric tensor for cylindrically shaped pulses with uniform energy density. Building upon that framework, we derive the complete set of geodesics with zero angular velocity. We show that perturbations in particle trajectories may be observed in gamma ray bursts. Also, deviations in the motion of moving particles are significantly larger than those previously found for particles that are initially at rest.
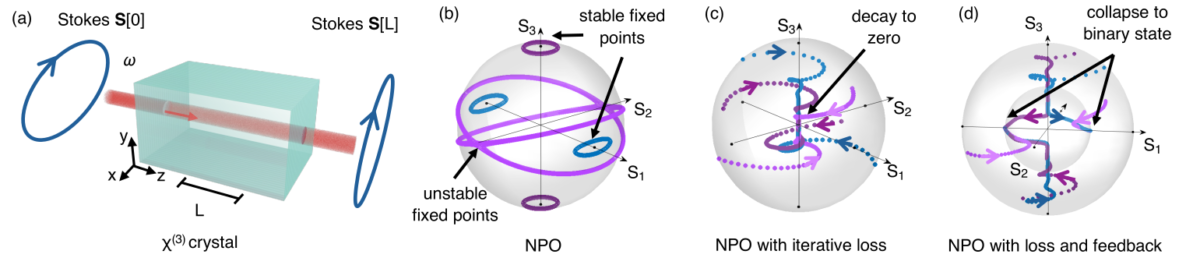
Ising Machine by Dimensional Collapse of Nonlinear Polarization Oscillators
https://journals.aps.org/prl/abstract/10.1103/qs29-2xqc
Phys. Rev. Lett. 135, 063801 – Published 4 August, 2025
Ising machines show promise as ultrafast hardware for optimizations encoded in Ising Hamiltonians but fall short in terms of success rate and performance scaling. Here, we propose a novel Ising machine that exploits the three-dimensional nature of nonlinear polarization oscillators to counteract these limitations. Based on the evolution of the optical polarization in third-order nonlinear media, the high-dimensional machine reaches the Ising ground state by the mechanism of “dimensional collapse”: the dynamics on the Poincaré sphere undergoes a self-induced collapse into polarization fixed points mapping an Ising spin. Collapse from a spherical to a binary spin occurs when the polarization oscillator experiences iterative loss and anisotropic feedback. The photonic setup consists of polarization modulated pulses in a 𝜒(3) crystal subject to measurement and feedback. We numerically demonstrate the polarization machine achieves enhanced success probability on benchmark graphs and an exponential improvement in performance scaling with respect to coherent Ising machines due to its high-dimensional operation. The proposed Ising machine paves the way for a new class of Ising solvers with enhanced computing capabilities.